Persistent Homology

A persistent Homology is a tool used for gaining insights into the topological invariants of a high-dimensional manifold (an n-dimensional torus) using computers. The manifolds embedded in higher-dimensional Euclidean spaces are represented with the help of uniformly sampled data points (Position vectors or arrows drawn from origin to surface of the manifold). In Persistent Homology, a sequence of topological structures is associated with the sampled data points, which in turn is assigned with a sequence of free Abelian groups. Persistent homology utilizes functors to associate a topological structure with a free abelian group that carries information about the invariants. Since the free abelian groups generated with the help of a finite field have a structure similar to that of a vector space over the same finite field, we can leverage linear algebra tools in computing the topological invariants. The topological invariants are nothing but the different dimensional holes corresponding to a topological manifold. The 0,1 and 2-dimensional holes correspond to the number of connected components, hole (in the sense of hole through a circle), and void. For example, a sphere has one 2-dimensional hole, one 0-dimensional hole and no 1-dimensional hole. A circle has one 0-dimensional hole, one 1-dimensional hole and no 2-dimensional holes. Rips filtration, which is a one-parameter filtration, is utilized in generating a sequence of topological spaces related to each other by inclusion maps. As the parameter corresponding to the Rips filtration increases, the topological structure associated with the data points change and new holes get generated and destroyed. The parameter value of Rips filtration at which an n-dimensional hole is created is phrased as its birth time, and the parameter value at which it gets destroyed is known as its death time. The persistence corresponding to a hole is the difference between its death and birth time.  

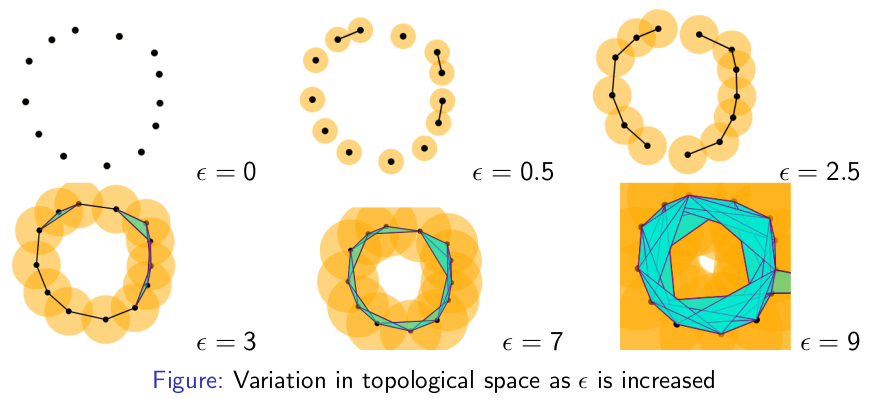
To understand the variation in parameter, consider the figure below. In the figure \( \epsilon \) is the parameter of the rips filtration  

A 1-dimensional hole gets created at \( \epsilon = 7\) and a 0-dimensional hole gets destroyed at \( \epsilon=7\). A persistent diagram logs the information of holes getting generated and destroyed by using their birth and death times. The persistence of a hole is the difference between its death and birth time. An n-dimensional hole with high persistence indicates the presence of an n-dimensional hole in the manifold from which the data points are sampled from.  

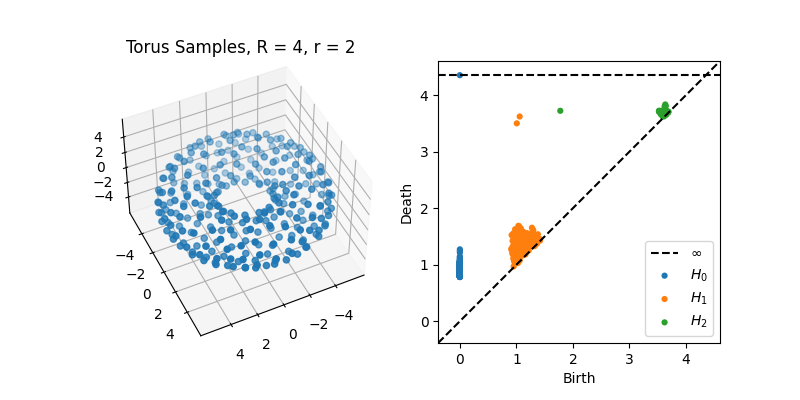
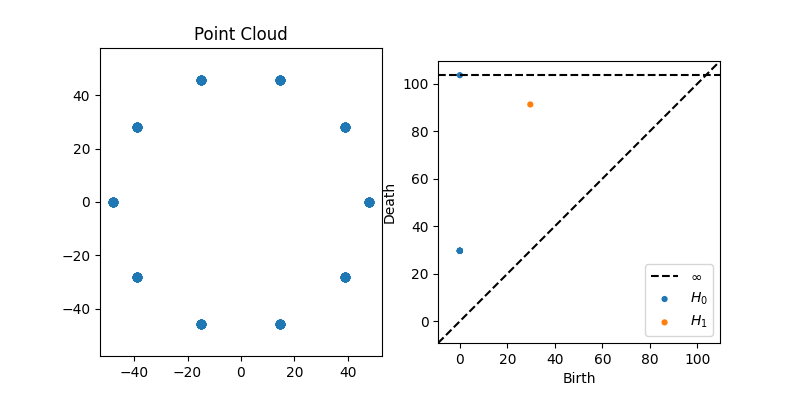
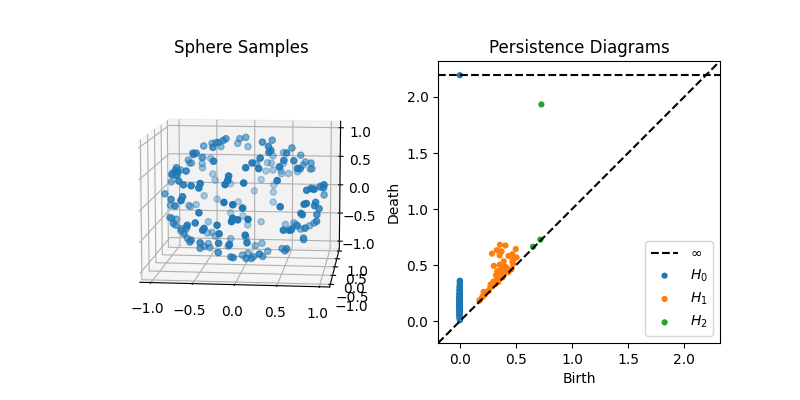
Some examples of peristence diagrams corresponding to some typical point clouds are shown below.