QuITO: Examples
This page provides several examples showcasing the performance of QuITO v.2. These examples are lifted from GDC2024, and we refer to this (openly accessible) source for the precise descriptions of the problems.
The Aly-Chan problem
The formal statement of the benchmark Aly-Chan optimal control problem is in Subsection 4.2 of GDC2024. Here we showcase some figures.
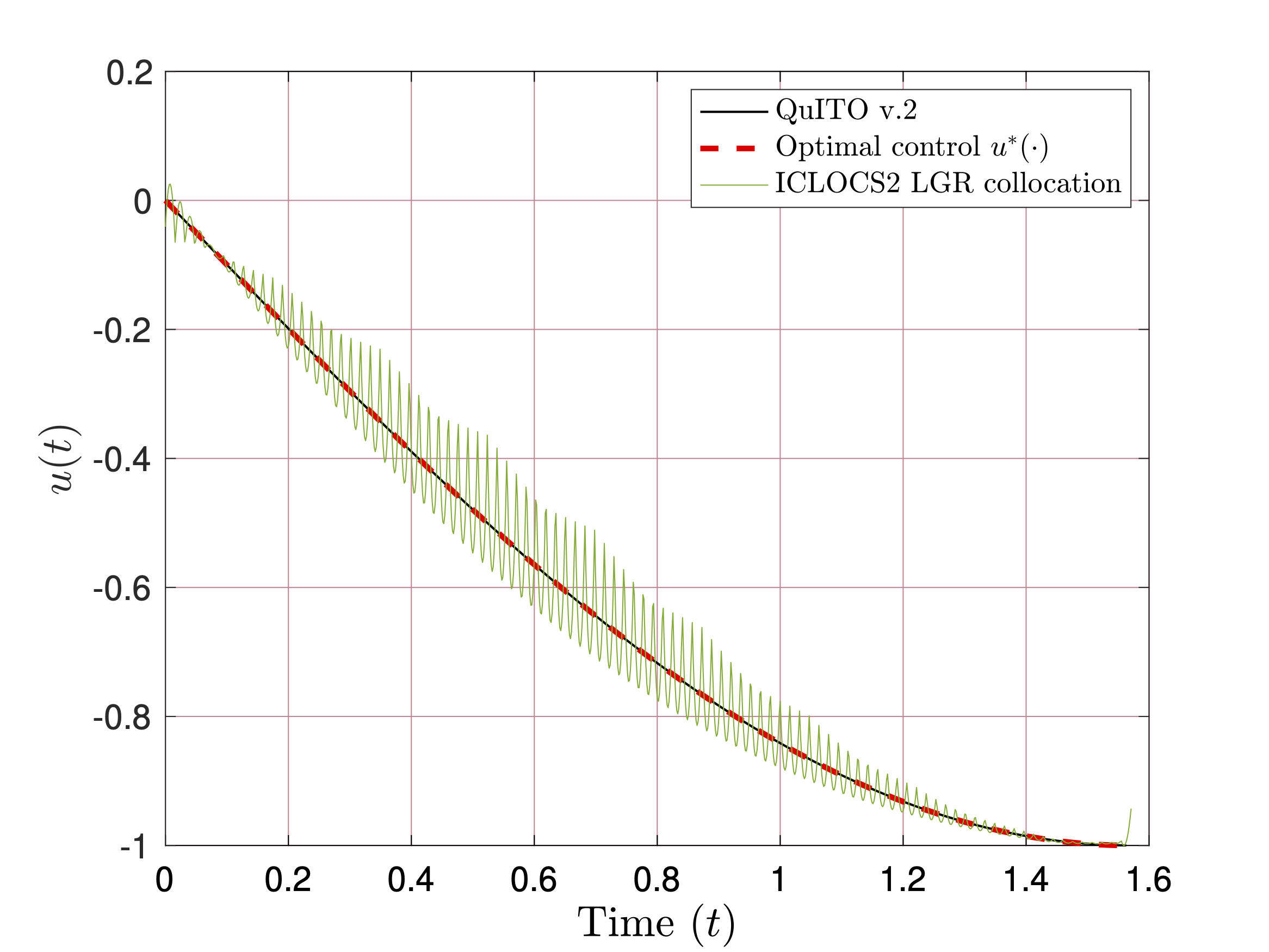
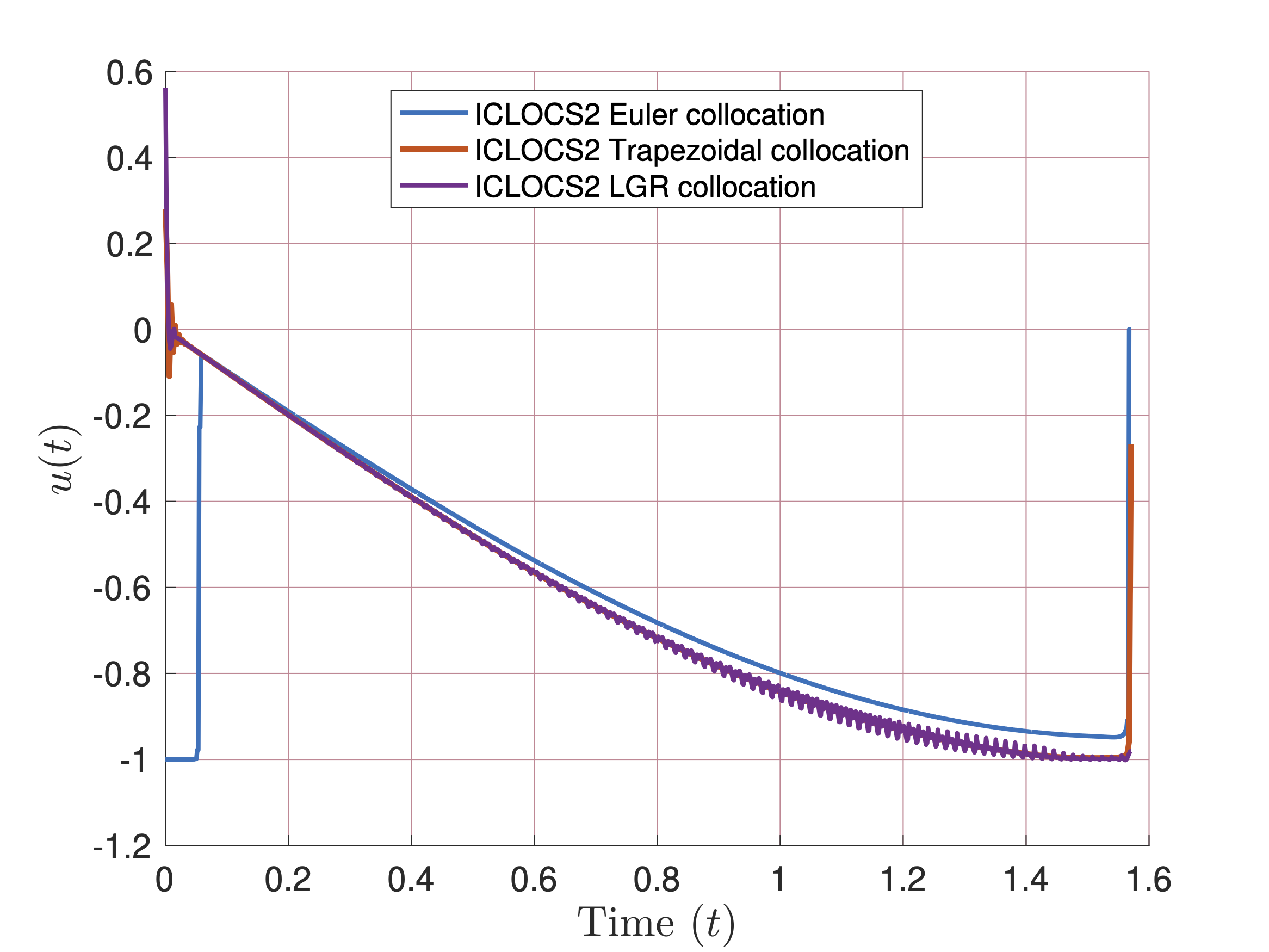
The first figure shows trajectories obtained via QuITO v.2 and by ICLOCS2 (employing LGR collocation using Legendre polynomials) for state and control representation for the Aly-Chan problem. The second one depicts Euler, Trapezoidal, and Hermite-Simpson collocation using piecewise cubic hermite interpolating polynomial for the state and control representations for the same problem.
The Bressan problem
The formal statement of the benchmark Bressan optimal control problem is in Subsection 5.2 of GDC2024. Here we showcase some figures.
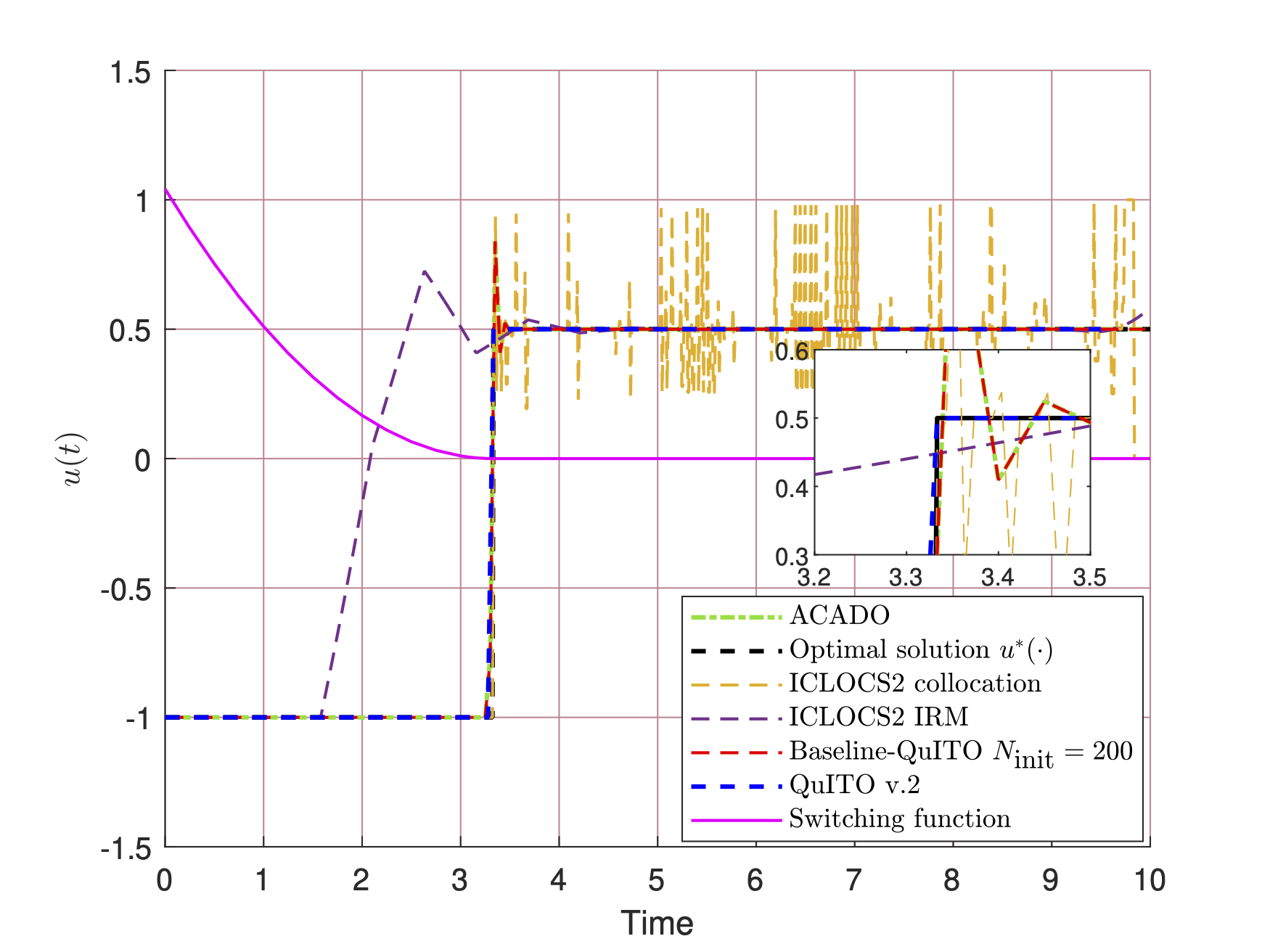
The preceding figure shows the performance of QuITO v.2 against ACADO, several techniques included in ICLOCS2, and the (version 1) baseline QuITO (that does not feature mesh refinement).
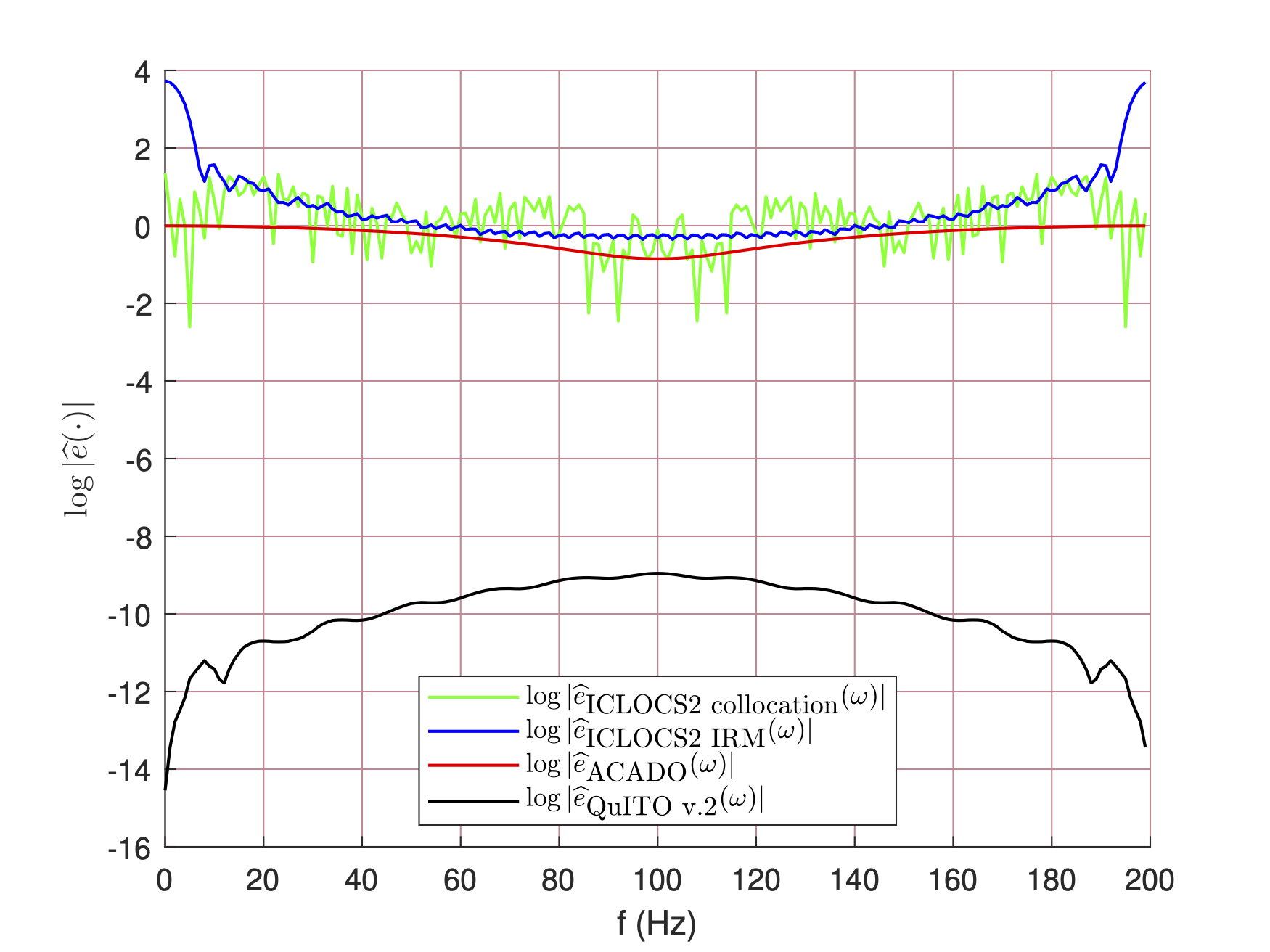
The figure above shows the DFT plot of absolute errors of the preceding techniques in log scale.
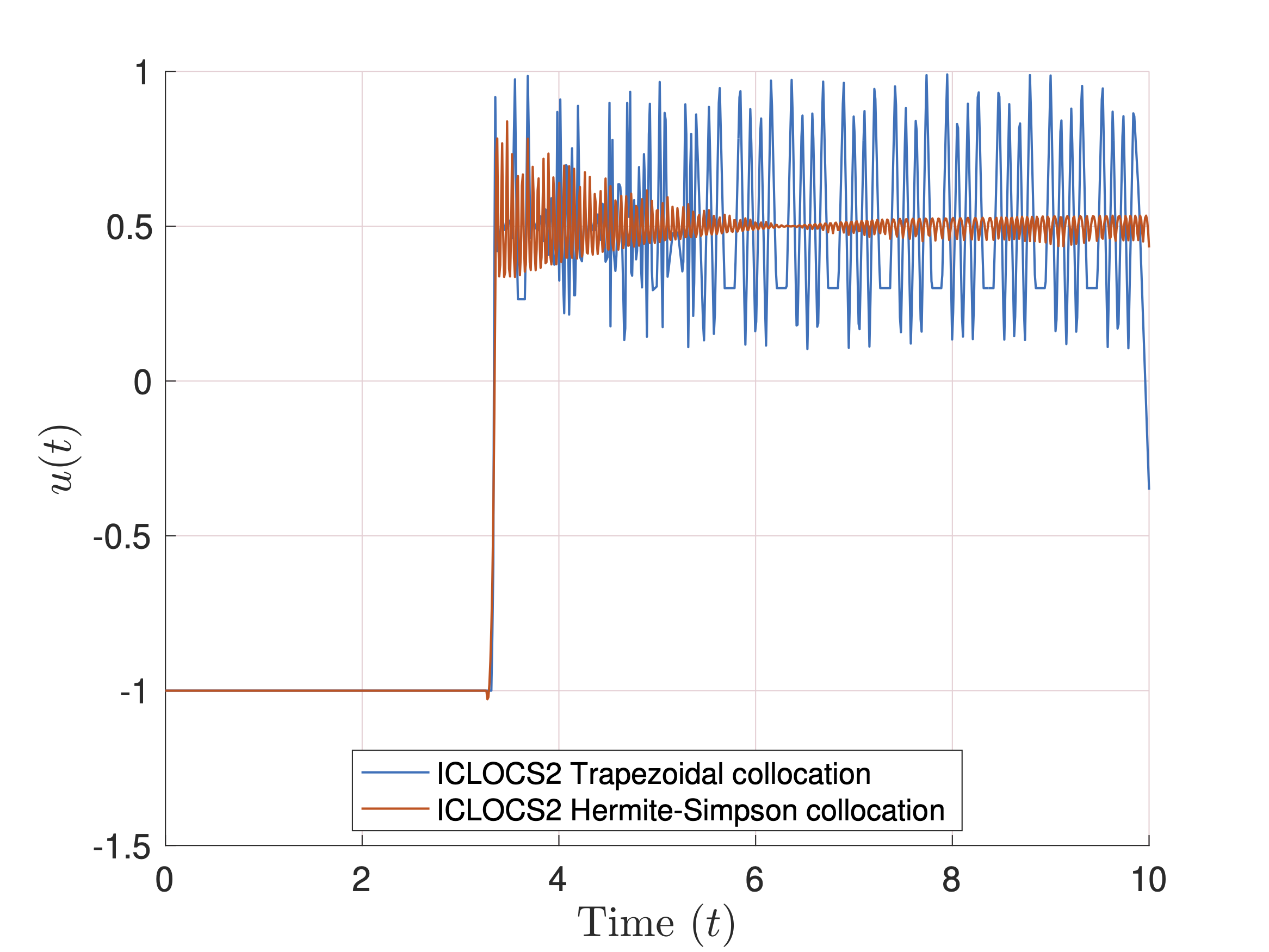
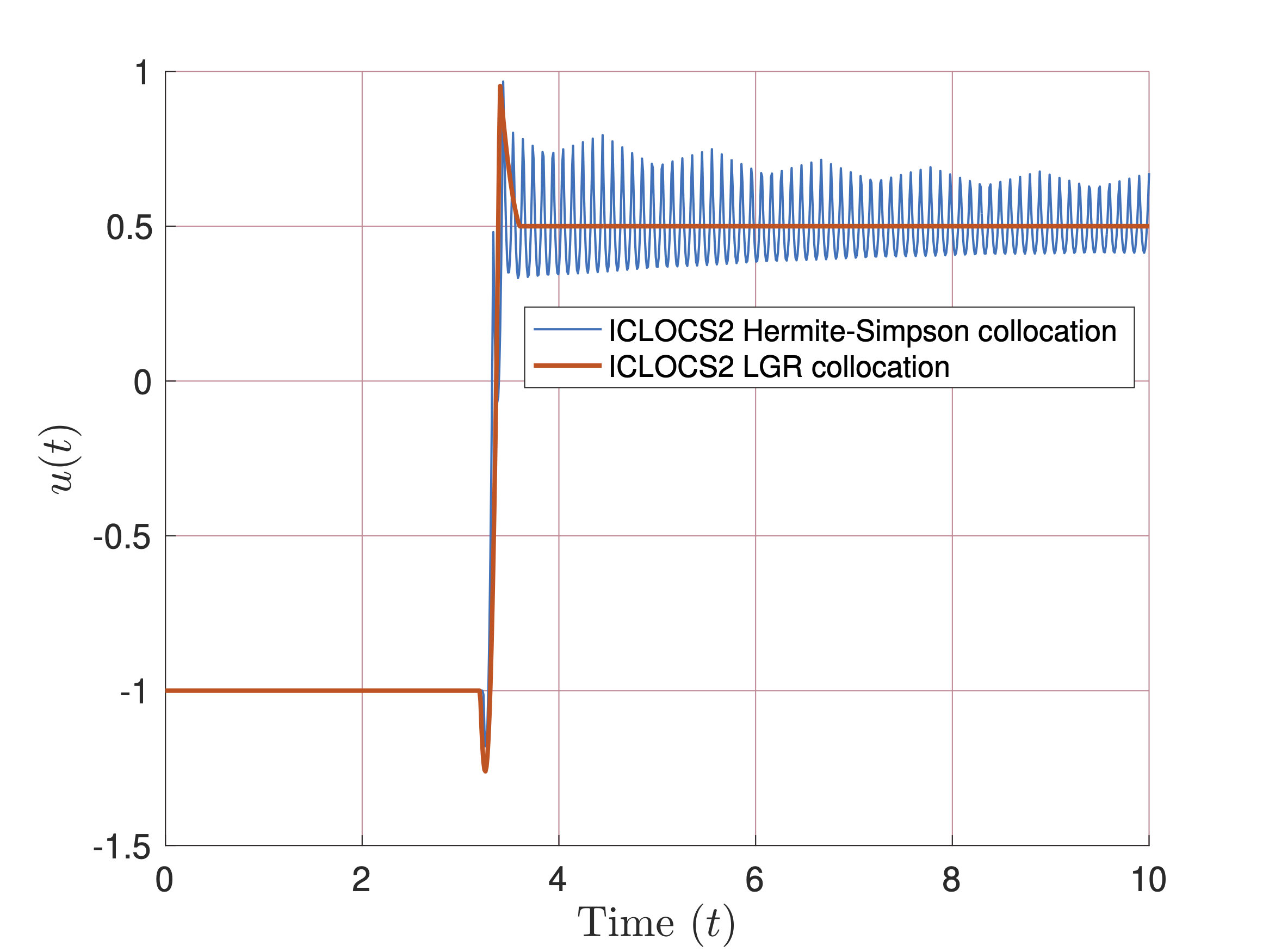
The first figure above shows the control trajectories obtained by Trapezoidal and Hermite-Simpson collocation using piecewise cubic Hermite interpolating polynomial for state and control representation. The second figure shows trajectories obtained by Hermite-Simpson and LGR collocation (via ICLOCS2) using piecewise cubic and Legendre polynomial respectively for state and control representation. ICLOCS2 was employed for both the cases.
A catalyst mixing problem
The formal statement of a singular catalyst mixing optimal control problem is in Subsection 5.3 of GDC2024. Here we showcase some figures.
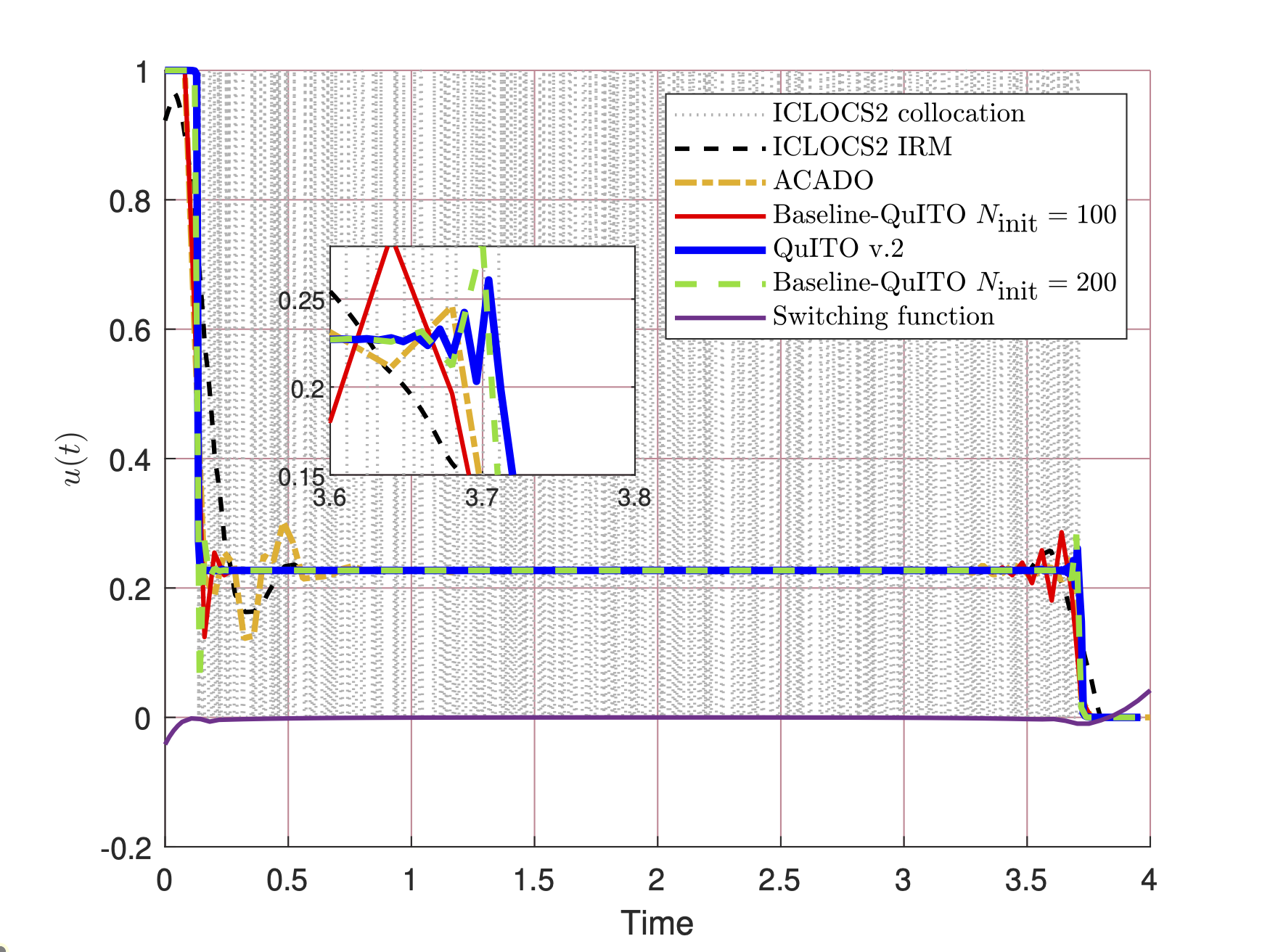
The preceding figure shows the performance of QuITO v.2 against ACADO, several techniques included in ICLOCS2, and the (version 1) baseline QuITO (that does not feature mesh refinement).
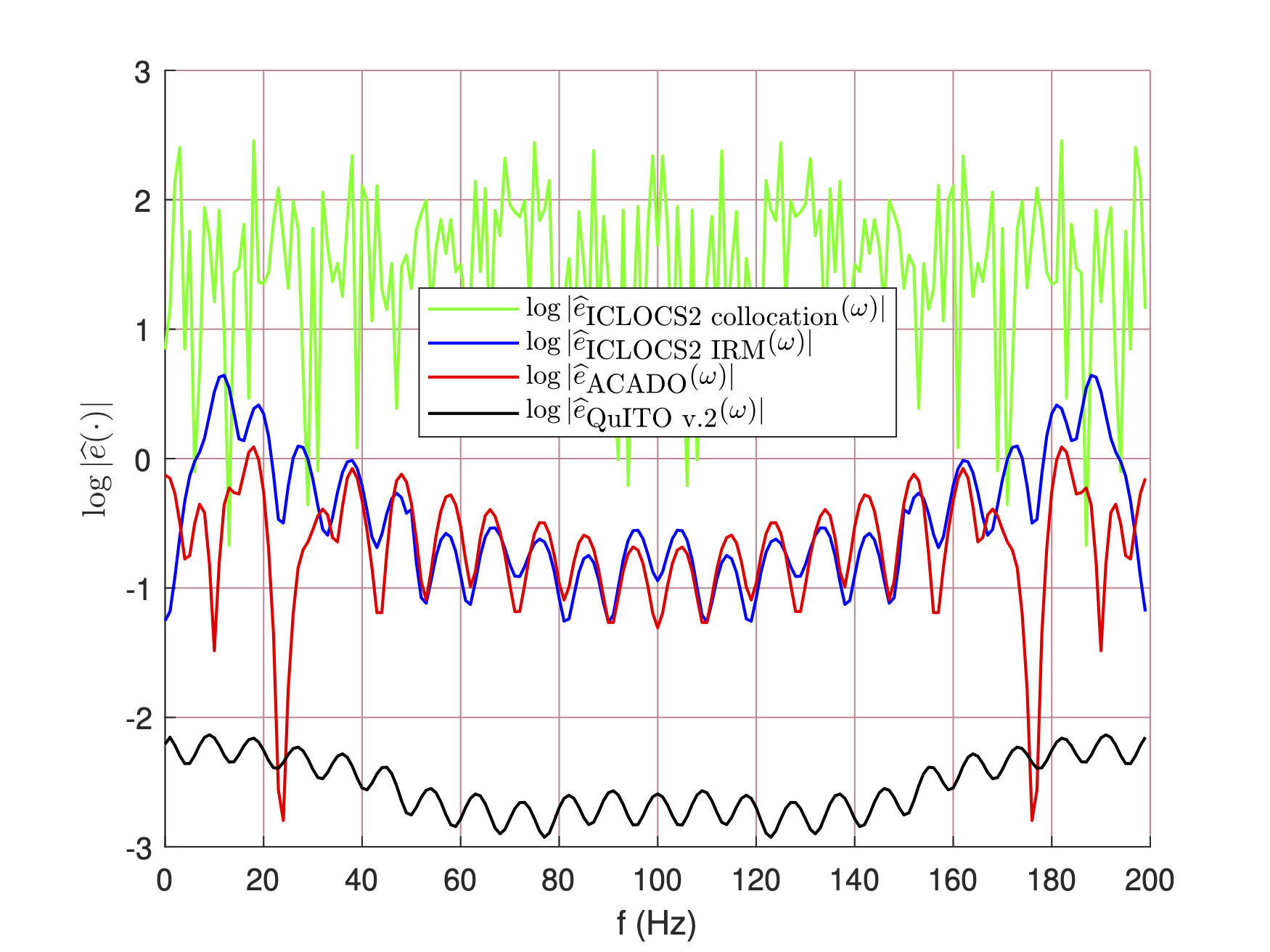
The figure above shows the DFT plot of absolute errors of the preceding techniques in log scale.
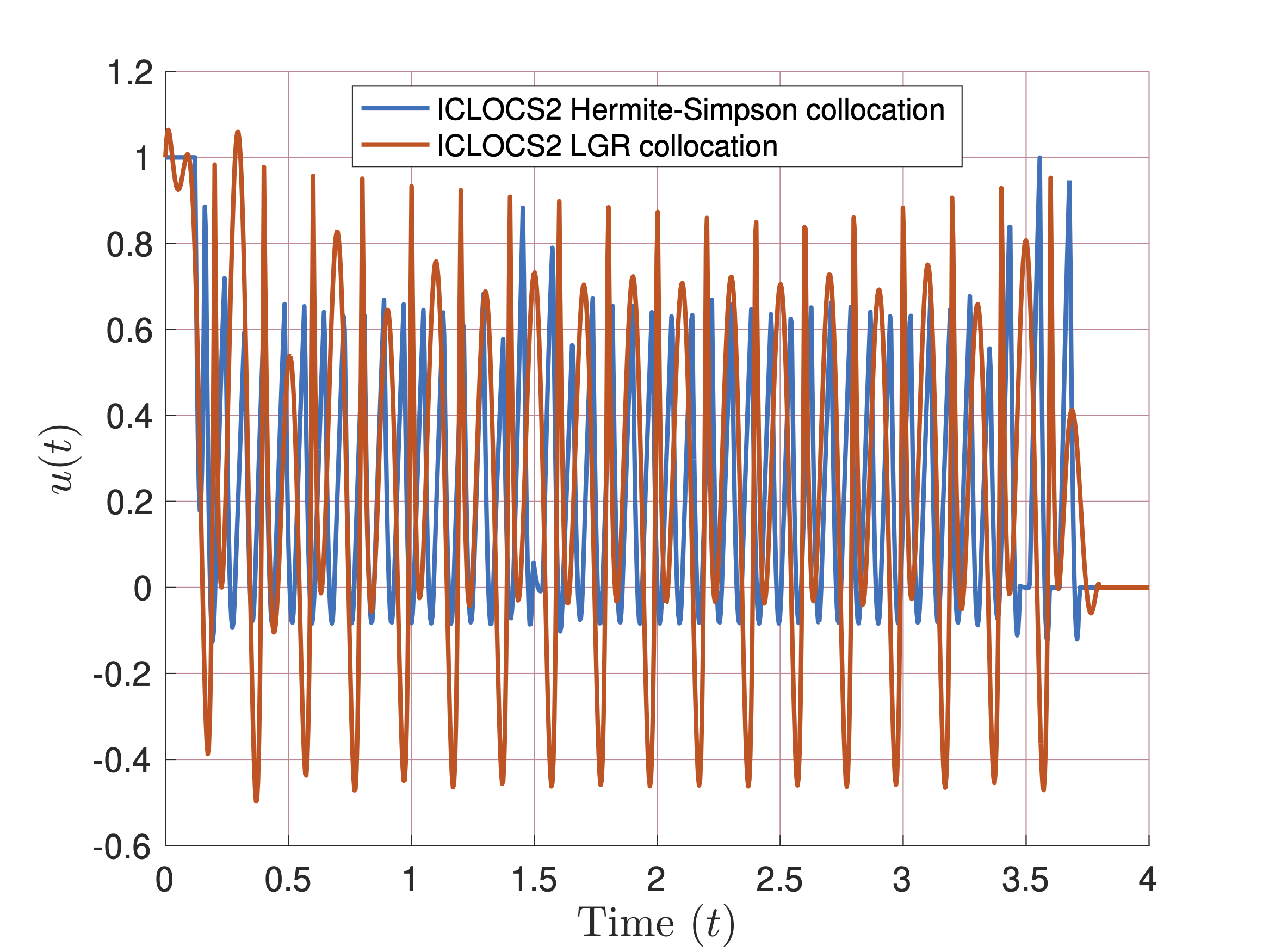
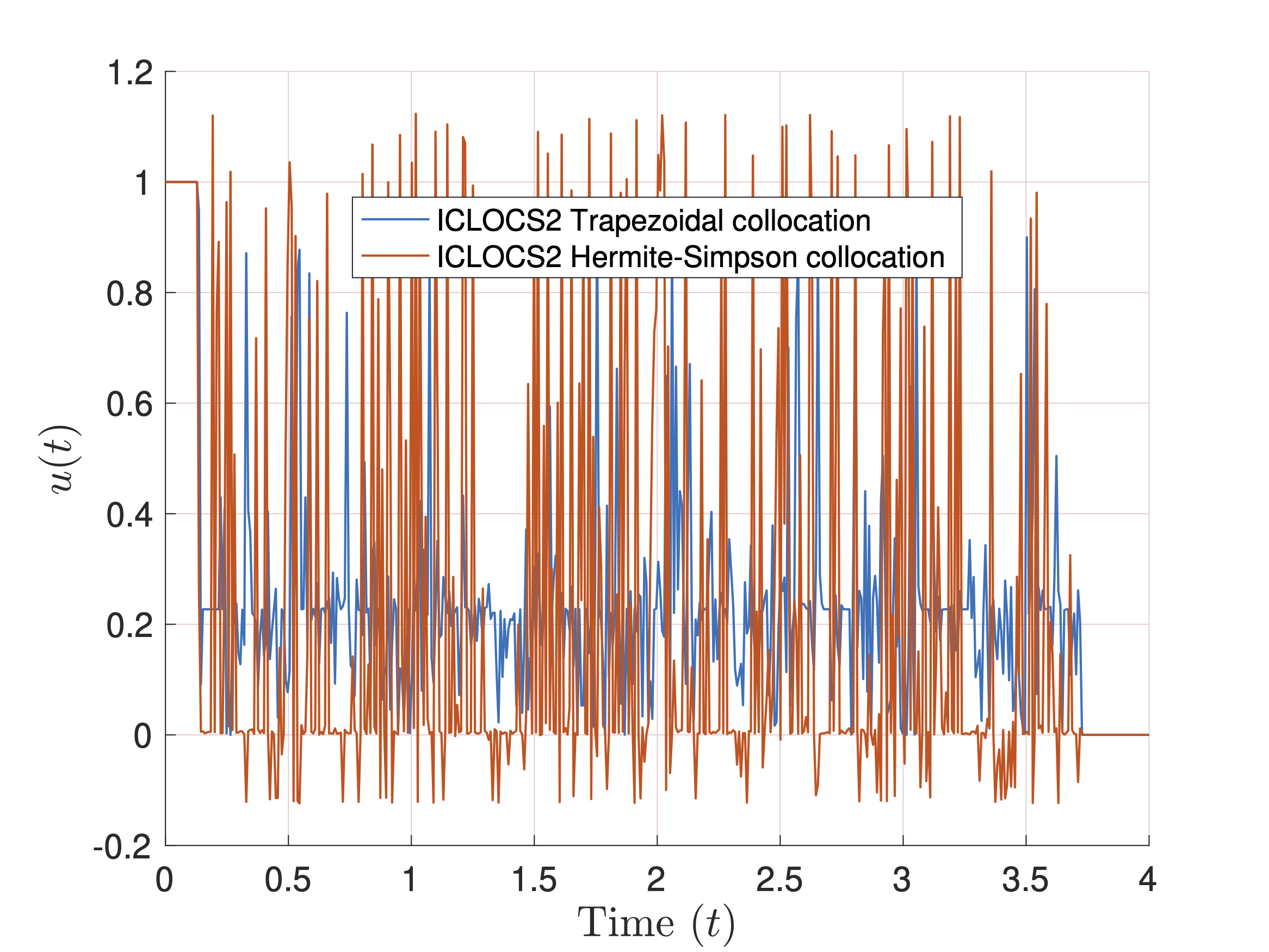
Control trajectories obtained from Trapezoidal and Hermite-Simpson collocation using piecewise cubic Hermite interpolating polynomials for the state and control representations in ICLOCS2 are shown in the first figure. Control trajectories obtained from Hermite-Simpson and LGR collocation using piecewise cubic and Legendre polynomials, respectively, for the state and control representations are shown in the second figure.
A SIRI epidemic problem
The formal statement of a SIRI epidemic optimal control problem is in Subsection 5.4 of GDC2024. Here we showcase a figure.
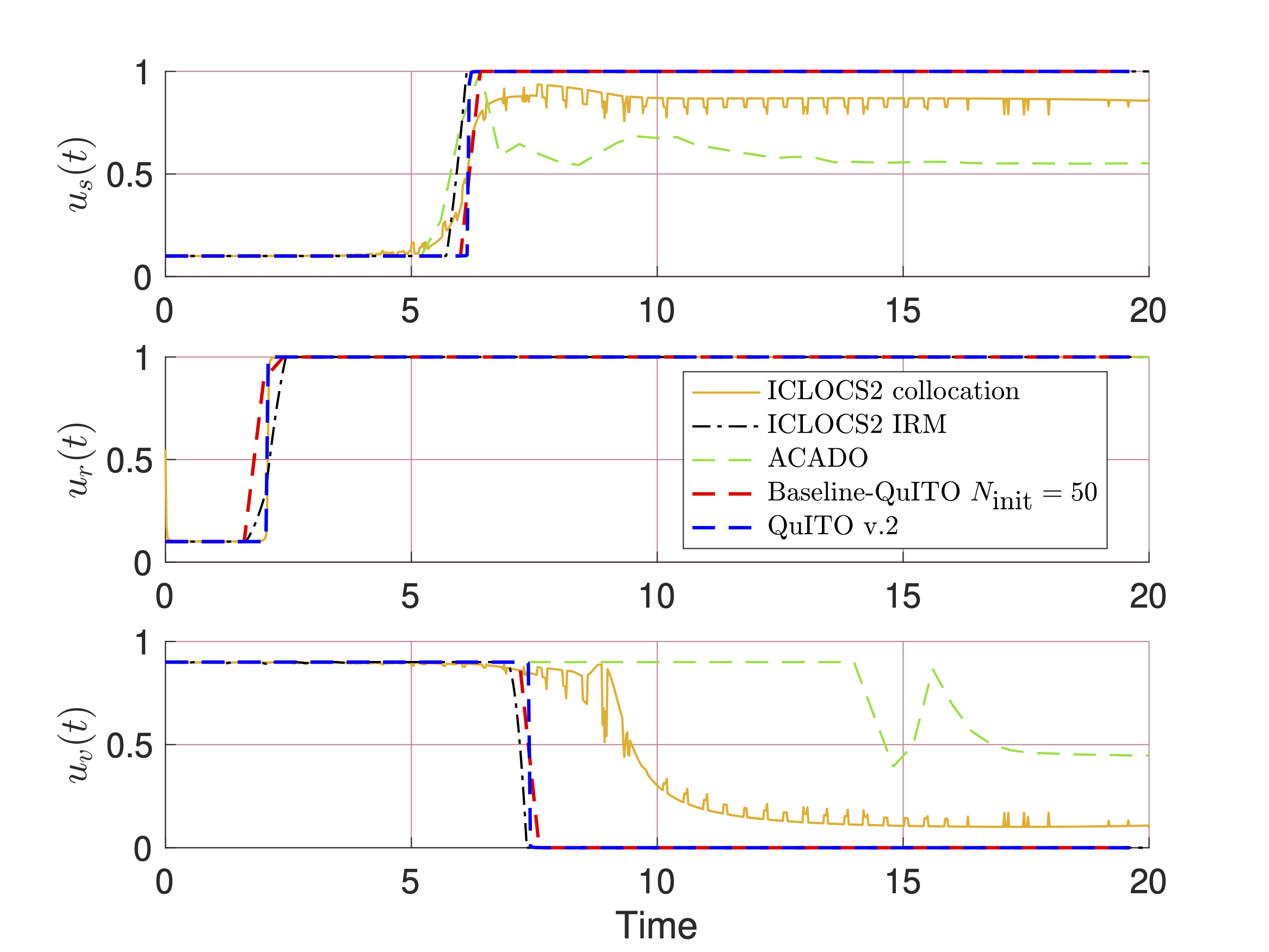
Control trajectories obtained from QuITO v.2, the collocation and IRM methods of ICLOCS2, and baseline QuITO.